
Abstract
R package developers traditionally rely on ad-hoc benchmarking (empirical timings and visual plots) to understand their code's asymptotic performance. We lack a framework for systematically testing the computational complexity of a function, which is crucial for identifying and implementing speed improvements in R code. testComplexity attempts to address this by providing a suite of functions for asymptotic complexity classification.
Since algorithms are used in every sphere of research, this package potentially caters to all variants of R-users. It has been specifically tested on ones ranging from changepoint detection and sorting to constrained optimal segmentation and partitioning, besides common base R functions such as substring and gregexpr.
Setup
Use devtools or remotes to fetch the package from the GitHub repository:
if(!require(devtools)) install.packages("devtools") devtools::install_github("Anirban166/testComplexity")
if(!require(remotes)) install.packages("remotes") remotes::install_github("Anirban166/testComplexity")
Function Map
testComplexity @ returns @ type @ commit-branch(es)
├──> asymptoticTimings : data.frame timings quantifier master
│ ├──> asymptoticTimeComplexityClass : ├──> string ↑ complexity classifier master
│ └──> plotTimings : └──> ggplot object ↑ plotter master/Plotfunc
│
├──> asymptoticMemoryUsage : data.frame memory-usage quantifier Memtest
│ ├──> asymptoticMemoryComplexityClass : ├──> string ↑ complexity classifier Memtest
│ └──> plotMemoryUsage : └──> ggplot object ↑ plotter Memtest/Plotfunc
│
├──> asymptoticComplexityClass : string complexity classifier Generalizedcomplexity
│ └──> asymptoticComplexityClassifier : ↑ string ↑ complexity classifier Generalizedcomplexity
│
├──> expect_complexity_class : -/- test function Testfunc
│ └──> expect_time_complexity : -/- ↑ test function Testfunc
│ ├──> expect_linear_time : -/- ↑↑ test function Testfunc
│ ├──> expect_loglinear_time : -/- ↑↑ test function Testfunc
│ └──> expect_quadratic_time : -/- ↑↑ test function Testfunc
│
└──> testthat
├──> testsfortestComplexity unit-tester All branches
├──> testsforConstrainedchangepointmodelalgos unit-tester Testfunc
└──> testsforRegularfunctions unit-tester Testfunc
Usage
To get started, please check the general vignette which highlights all features, categorizes the different functions available, and describes their functionality through textual elucidations and a running example case.
For a quick overview of the main functionality (obtaining quantified benchmarks and subsequently computing the time/memory complexity class), please check the examples below.
- To obtain the benchmarked timings/memory-allocations against specified data sizes, pass the required algorithm as a function of
NtoasymptoticTimings()/asymptoticMemoryUsage():
library(data.table)
# Example 1 | Applying the bubble sort algorithm to a sample of 100 elements: (expected -> quadratic time & constant memory complexity)
bubble.sort <- function(elements.vec) {
n <- length(elements.vec)
for(i in 1:(n - 1)) {
for(j in 1:(n - i)) {
if(elements.vec[j + 1] < elements.vec[j]) {
temp <- elements.vec[j]
elements.vec[j] <- elements.vec[j + 1]
elements.vec[j + 1] <- temp
}
}
}
return(elements.vec)
}
df.bubble.time <- asymptoticTimings(bubble.sort(sample(1:100, N, replace = TRUE)), data.sizes = 10^seq(1, 3, by = 0.5))
data.table(df.bubble.time)
Timings Data sizes
1: 91902 10
2: 39402 10
3: 34701 10
4: 33101 10
5: 33201 10
---
496: 64490501 1000
497: 59799101 1000
498: 63452200 1000
499: 62807201 1000
500: 59757102 1000
df.bubble.memory <- asymptoticMemoryUsage(bubble.sort(sample(1:100, N, replace = TRUE)), data.sizes = 10^seq(1, 3, by = 0.1))
data.table(df.bubble.memory)
Memory usage Data sizes
1: 87800 10.00000
2: 2552 12.58925
3: 2552 15.84893
4: 2552 19.95262
5: 2552 25.11886
---
17: 7472 398.10717
18: 8720 501.18723
19: 10256 630.95734
20: 12224 794.32823
21: 14696 1000.00000# Example 2 | Testing PeakSegPDPA, an algorithm for constrained changepoint detection: (expected -> log-linear time and memory complexity)
data.vec <- rpois(N, 1)
df.PDPA.time <- asymptoticTimings(PeakSegOptimal::PeakSegPDPA(count.vec = data.vec, max.segments = 3L), data.sizes = 10^seq(1, 4, by = 0.1))
&data.table(df.PDPA.time)
Timings Data sizes
1: 248701 10
2: 120302 10
3: 125701 10
4: 133301 10
5: 146500 10
---
696: 405597501 10000
697: 408335001 10000
698: 338544401 10000
699: 404081901 10000
700: 399575501 10000
df.PDPA.memory <- asymptoticMemoryUsage(PeakSegOptimal::PeakSegPDPA(count.vec = data.vec, max.segments = 3L), data.sizes = 10^seq(1, 4, by = 0.1))
data.table(df.PDPA.memory)
Memory usage Data sizes
1: 6256 10.00000
2: 7024 12.58925
3: 7432 15.84893
4: 8560 19.95262
5: 9496 25.11886
---
25: 447792 2511.88643
26: 562336 3162.27766
27: 706512 3981.07171
28: 887792 5011.87234
29: 1116240 6309.57344- To estimate the corresponding time/memory complexity class, pass the obtained data frame onto
asymptoticTimeComplexityClass()/asymptoticMemoryComplexityClass():
# Example 1 | Applying the bubble sort algorithm to a sample of 100 elements: (expected -> quadratic time & constant memory complexity) asymptoticTimeComplexityClass(df.bubble.time) [1] "quadratic" asymptoticMemoryComplexityClass(df.bubble.memory) [1] "constant"
# Example 2 | Testing PeakSegPDPA, an algorithm for constrained changepoint detection: (expected -> log-linear time and memory complexity) asymptoticTimeComplexityClass(df.PDPA.time) [1] "loglinear" asymptoticMemoryComplexityClass(df.PDPA.memory) [1] "loglinear"
- Combine the functions if you only require the complexity class:
# Example 3 | Testing the time complexity of the quick sort algorithm: (expected -> log-linear time complexity) asymptoticTimeComplexityClass(asymptoticTimings(sort(sample(1:100, N, replace = TRUE), method = "quick" , index.return = TRUE), data.sizes = 10^seq(1, 3, by = 0.5))) [1] "loglinear"
# Example 4 | Allocating a square matrix (N*N dimensions): (expected -> quadratic memory complexity) asymptoticMemoryComplexityClass(asymptoticMemoryUsage(matrix(data = N:N, nrow = N, ncol = N), data.sizes = 10^seq(1, 3, by = 0.1))) [1] "quadratic"
Check this screencast for a demonstration of time complexity testing on different sorting algorithms over a test session.
Plotting
For obtaining a visual description of the trends followed between runtimes/memory-usage vs data sizes in order to visually diagnose/verify the complexity result(s), simple plots can be crafted. They are roughly grouped into:
-
Single Plots
Individual plots can be obtained by passing the data frame returned by the quantifying functions toplotTimings()/plotMemoryUsage()for time/memory cases respectively:
# Timings plot for PeakSegDP::cDPA
df <- asymptoticTimings(PeakSegDP::cDPA(rpois(N, 1), rep(1, length(rpois(N, 1))), 3L), data.sizes = 10^seq(1, 4))
plotTimings(df.time, titles = list("Timings", "PeakSegDP::cDPA"), line.color = "#ffec1b", point.color = "#ffec1b", line.size = 1, point.size = 1.5)
# Equivalent ggplot object:
df <- asymptoticTimings(PeakSegDP::cDPA(rpois(data.sizes, 1), rep(1, length(rpois(data.sizes, 1))), 3L), data.sizes = 10^seq(1, 4))
ggplot(df, aes(x = `Data sizes`, y = Timings)) + geom_point(color = ft_cols$yellow, size = 1.5) + geom_line(color = ft_cols$yellow, size = 1) + labs(x = "Data sizes", y = "Runtime (in nanoseconds)") + scale_x_log10() + scale_y_log10() + ggtitle("Timings", "PeakSegDP::cDPA") + hrbrthemes::theme_ft_rc()# Memory Usage plot for PeakSegDP::cDPA
df <- asymptoticMemoryUsage(PeakSegDP::cDPA(rpois(N, 1), rep(1, length(rpois(N, 1))), 3L), data.sizes = 10^seq(1, 6, by = 0.1))
plotMemoryUsage(df.memory, titles = list("Memory Usage", "PeakSegDP::cDPA"), line.color = "#ffec1b", point.color = "#ffec1b", line.size = 1, point.size = 2)
# Equivalent ggplot object:
ggplot(df, aes(x = `Data sizes`, y = `Memory usage`)) + geom_point(color = ft_cols$yellow, size = 2) + geom_line(color = ft_cols$yellow, size = 1) labs(x = "Data sizes", y = "Memory usage (in bytes)") + scale_x_log10() + scale_y_log10() + ggtitle("Memory Usage", "PeakSegDP::cDPA") + hrbrthemes::theme_ft_rc()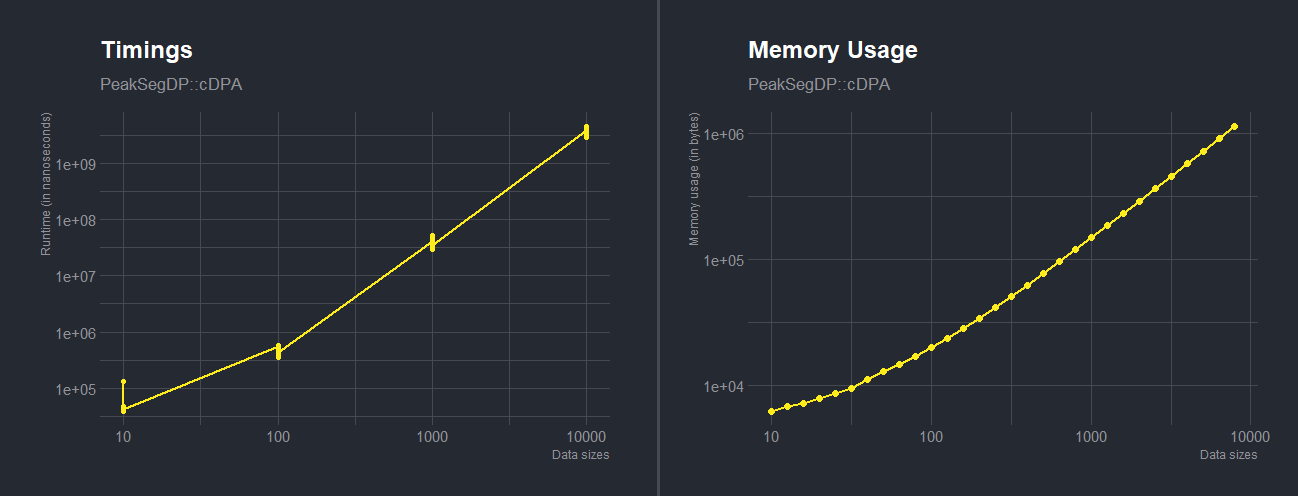
-
Comparison Plots
In order to visually compare different algorithms based on the benchmarked metrics returned as a data frame by the quantifiers, one can appropriately add a third column (to help distinguish by aesthetics based on it) with a unique value for each of the data frames, combine them using anrbind()and then plot the resultant data frame using suitable aesthetics, geometry, scale, labels/titles etc. via a ggplot:
df.substring <- asymptoticTimings(substring(paste(rep("A", N), collapse = ""), 1:N, 1:N), data.sizes = 10^seq(1, 4, by = 0.5))
asymptoticTimeComplexityClass(df.substring)
[1] "linear"
df.PeakSegPDPA <- asymptoticTimings(PeakSegOptimal::PeakSegPDPA(rpois(N, 1),rep(1, length(rpois(N, 1))), 3L), data.sizes = 10^seq(1, 4, by = 0.5), max.seconds = 1)
asymptoticTimeComplexityClass(df.PeakSegPDPA)
[1] "loglinear"
df.cDPA <- asymptoticTimings(PeakSegDP::cDPA(rpois(N, 1), rep(1, length(rpois(N, 1))), 3L), data.sizes = 10^seq(1, 4, by = 0.5), max.seconds = 5)
asymptoticTimeComplexityClass(df.cDPA)
[1] "quadratic"
df.gregexpr <- asymptoticTimings(gregexpr("a", paste(collapse = "", rep("ab", N)), perl = TRUE), data.sizes = 10^seq(1, 4, by = 0.5))
asymptoticTimeComplexityClass(df.gregexpr)
[1] "linear"
df.fpop <- asymptoticTimings(fpop::Fpop(rnorm(N), 1), data.sizes = 10^seq(1, 4, by = 0.5))
asymptoticTimeComplexityClass(df.fpop)
[1] "loglinear"
df.opart <- asymptoticTimings(opart::opart_gaussian(rnorm(N), 1), data.sizes = 10^seq(1, 4, by = 0.5))
asymptoticTimeComplexityClass(df.opart)
[1] "quadratic"
df.substring$expr = "substring"
df.PeakSegPDPA$expr = "PeakSegPDPA"
df.cDPA$expr = "cDPA"
df.gregexpr$expr = "gregexpr"
df.fpop$expr = "fpop"
df.opart$expr = "opart"
plot.df <- rbind(df.substring, df.PeakSegPDPA, df.cDPA, df.gregexpr, df.fpop, df.opart)
ggplot(plot.df, aes(x = `Data sizes`, y = Timings)) + geom_point(aes(color = expr)) + geom_line(aes(color = expr)) + labs(x = "Data sizes", y = "Runtime (in nanoseconds)") + scale_x_log10() + scale_y_log10() + ggtitle("Timings comparison plot", subtitle = "Linear vs Log-linear vs Quadratic complexities") + ggthemes::theme_pander()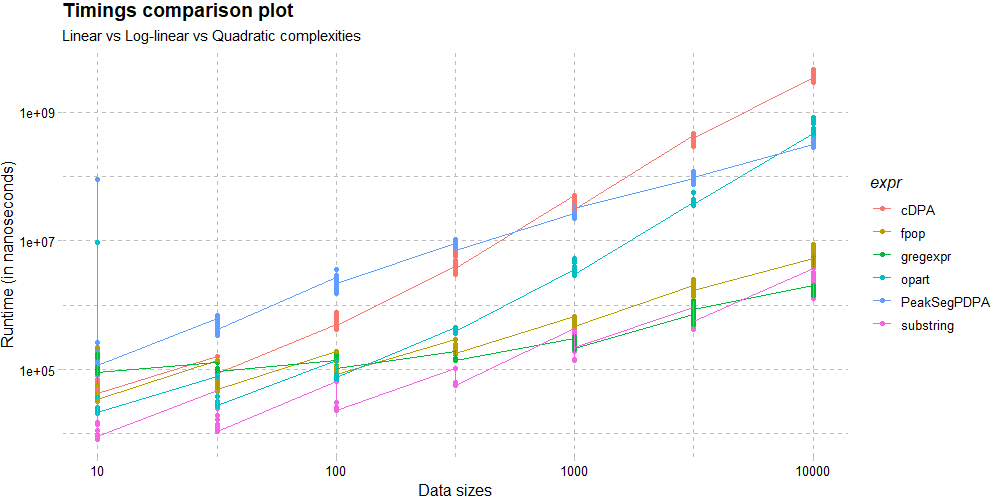
Including more functions (if applicable) and increasing the number of data sizes can lead to a more comprehensive outlook:
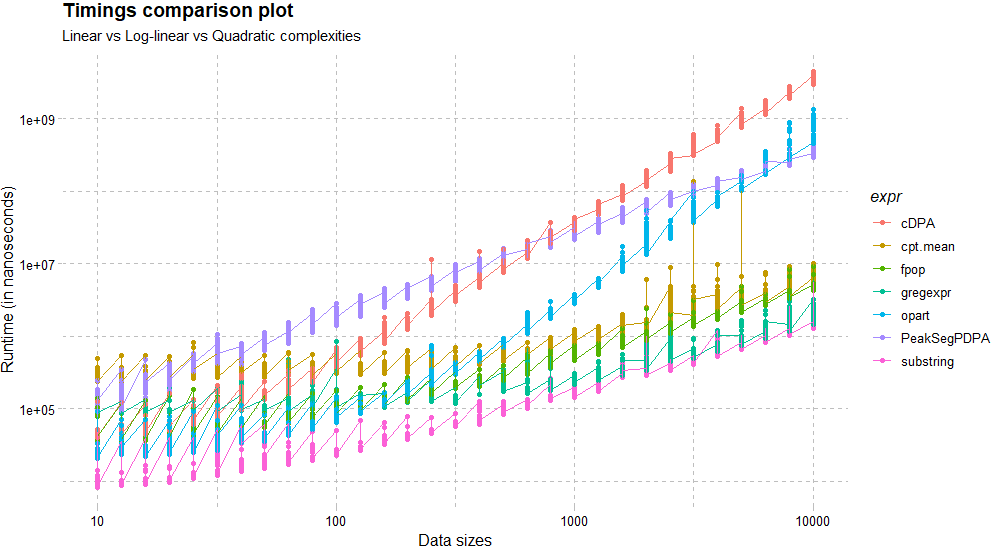
-
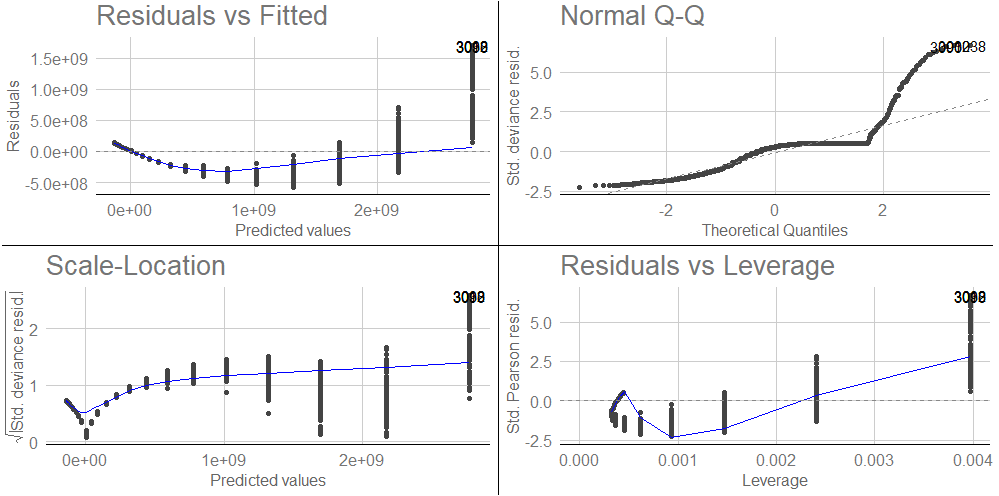
Generalized Linear Model based Plots
ggfortify(an extension ofggplot2) can be used to produce diagnostic plots for generalized linear models with the same formulae as used in the complexity classification functions:
library(ggfortify) df <- asymptoticTimings(PeakSegDP::cDPA(rpois(N, 1), rep(1, length(rpois(N, 1))), 3L), data.sizes = 10^seq(1, 4 by = 0.1)) glm.plot.obj <- glm(Timings~`Data sizes`, data = df) ggplot2::autoplot(stats::glm(glm.plot.obj)) + ggthemes::theme_gdocs()
Benchmarking
-
microbenchmark::microbenchmark()is used to obtain the time results intestComplexity::asymptoticTimings()for precision and convenience of having the benchmarks as a data frame.
-
bench::bench_memory()is used to compute the size of memory allocation intestComplexity::asymptoticMemoryUsage().
Testing
-
Functions
The routines considered for testing the package's functionality are listed below.
A dedicated vignette-based article for each can be found via the ‘Articles’ section, accessible from this website’s navigation bar at the top.
-
Unit Testing
Test cases for testComplexity functions that utilize testthat can be found here.
-
Code Coverage
Tested usingcovr::package_coverage()both locally and via codecov, with 100% coverage attained.
-
OS Support
Windows is the native OS this package is developed and tested on. However, RCMD checks are run on latest versions of MacOS and Ubuntu as well.
Note that the use ofbench::bench_memory()overcomes the Windows-only OS limitation for memory complexity testing observed inGuessCompx::CompEst()as it successfully runs on other operating systems.


