Generalized complexity classification

As discussed with my mentor Toby Dylan Hocking over a call, he made a point to adapt an example to classify the complexity between a specified output parameter in relation to the data sizes, which sparked the need for a function via which we could classify the complexity for any parameter (rather than timings or memory allocations) which would be a column of the data frame provided. This post discusses the making of the same, which I termed to be ‘Generalized complexity classification’.

Function Details : Parameters

The function accepts a data frame along with two column names of the data frame, which are to be the attributes with values for the output parameter (such as timings/memory-allocations) and data sizes respectively.

Function Details : Implementation

To recap, the complexity classification process uses glms with formulae between our output parameter (previously time/memory) values and corresponding data sizes, wherein cross-validation is applied to them to obtain the adjusted delta errors and the least error among the various fitted complexity-class models demarks the best complexity class.

In this version of my implementation, I had to create a fresh data frame with user-supplied column names from within it, and then subsequently pass it into the complexity classification logic inside asymptoticComplexityClassifier, through the helper function asymptoticComplexityClass. This issue revolves around it, which discusses why I had to follow that and what were the errors without this logic taken into account.

To summarize, there are two key points to take note of if you’re implementing this or a similar function:

• Column names of the passed data frame should match with the parameters passed inside the calls to the glms.
• They should be available in global scope, i.e. the columns of the data frame should be accessible directly to the glm scope and not via something of the order of data.df$col and data.df$col2, or with reference to the data frame.

If we use a RCMD check() on our package, it can be seen as a note that the bindings are non-existent for those parameters inside the plotting functions:

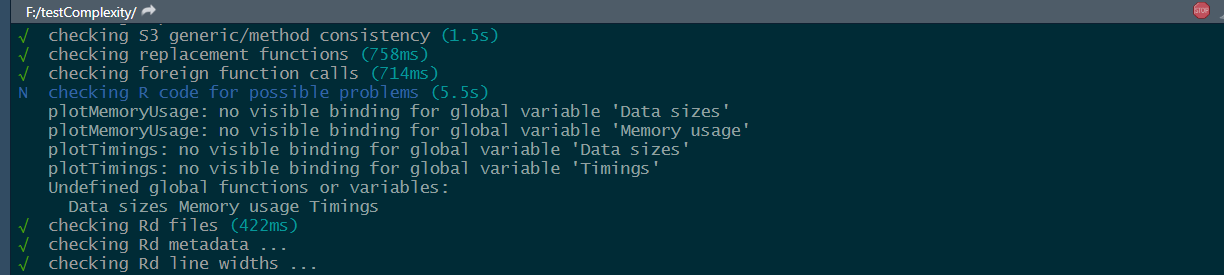
That’s because they aren’t captured like in the glm-based scope as in these complexity classification functions. Although it would seem legible to fix this for the plotters, the functionality for the complexity classifiers would break if these variables aren’t passed to the glms from the global scope. (the sole reason am ignoring this note pop-up, which isn’t an issue in development though)

Fixed global bindings via globals.R script mentioning those variables. CRAN requires notes to be taken care of, hence solving this minor problem was required.

Not wanting to repeat what’s been said before, I’ve excluded the basic implementation workflow mentioned in the complexity classifiers post but you can check the spoiler below for a quick reference to what’s been covered.

Function Details : Return value

The function returns a string signifying the complexity class, which falls in one of these complexities:
Constant, Linear, Log, Log-linear, Quadratic.

Usage

Since the computed data is already prevalent in the specified output parameter column of the data frame, we don’t need to use our quantifying functions or perform any benchmarks. Just specify the required columns for the output metric and data sizes apart from supplying the data frame to asymptoticComplexityClass:

# For example, lets consider PeakSegDP::cDPA() which we previously tested with the timings quantifier and obtained the expected quadratic complexity.
# Consider it as the data frame with already benchmarked data: (this is just to illustrate as per my convenience, we do not need to use our quantifiers here and any data frame would suffice) 
df <- asymptoticTimings(PeakSegDP::cDPA(rpois(data.sizes, 1), rep(1, length(rpois(data.sizes, 1))), 3L), data.sizes = 10^seq(1, 4, by = 0.5))
# Pass it, along with specifications for which column would be demark the output sizes and the data sizes: (the data frame can have any number of columns)
asymptoticComplexityClass(df, output.size = "Timings", data.size = "Data sizes")
[1] "quadratic"

Code

• asymptoticComplexityClass

  asymptoticComplexityClass = function(df, output.size, data.size)
  { # Check whether the columns specified by the user are prevalent in the data frame:
  if(class(df) == "data.frame" & output.size %in% colnames(df) & data.size %in% colnames(df))
  { # Create a data frame with user specified columns, to be passed onto asymptoticComplexityClassifier's glms:
    d <- data.frame('output' = df[[output.size]], 'size' = df[[data.size]])
    # Run the complexity classification on the above specified columnar values:
    asymptoticComplexityClassifier(d)
  }
  # Stop if specified columns don't exist:
  else stop("Input parameter must be a data frame containing the two specified columns passed as parameters")
  }
  

• asymptoticComplexityClassifier

  asymptoticComplexityClassifier = function(df)
  { # Check for required columns:
  if(class(df) == "data.frame" & 'output' %in% colnames(df) & 'size' %in% colnames(df))
  { # Create different glms of the formula output ~ size (x ~ y) for our data frame and extract the fits in different variables signifying a complexity class each:
    constant   <- glm(output~1,                  data = df); df['constant'] = fitted(constant)
    linear     <- glm(output~size,               data = df); df['linear'] = fitted(linear)
    log        <- glm(output~log(size),          data = df); df['log'] = fitted(log)
    loglinear  <- glm(output~size*log(size),     data = df); df['loglinear'] = fitted(loglinear)
    quadratic  <- glm(output~I(size^2),          data = df); df['quadratic'] = fitted(quadratic)
    # Create a list:
    model.list <- list()
    # Loop through different complexity classes:
    for(complexity.class in c('constant', 'log', 'linear', 'loglinear', 'quadratic'))
    { # Collect the fitted values in a list with corresponding complexity names:
      model.list[[complexity.class]] = eval(as.name(complexity.class))
    }  
    # Apply cross validation on each glm in the list via a lapply on a function based on our data frame and extract the adjusted delta error: (second parameter)
    cross.validated.errors <- lapply(model.list, function(x) cv.glm(df, x)$delta[2])
    # Select the model with the least error as our complexity class:
    best.model <- names(which.min(cross.validated.errors))
    # Print it:
    print(best.model)
  }
  # Stop if specified columns don't exist: 
  else stop("Input parameter must be a data frame containing the two specified columns passed as parameters")
  }
  

  rxoygen-documented versions:

• testComplexity/R/asymptoticComplexityClass
• testComplexity/R/asymptoticComplexityClassifier