A simple operation that is used in many applications (world map generation in games, fluid dynamics, graphical simulations etc.) is calculating the Euclidean distances between points. For instance, if point p₁ = (x₁, y₁) and point p₂ = (x₂, y₂), then the distance between those two points is .

For such a problem, one needs to compute the distances between points and find the total number of such distances that are within some threshold value, denoted by the epsilon character (ε), i.e. the total count of the number of occurrences distance(p₁, p₂) ≤ ε. As ε increases, the total number of points within ε should increase. (you can think of ε to be the search radius for each point)

Note that the Euclidean distance is reflexive, i.e., distance(p₁, p₂) = distance(p₂, p₁), but one must “double count” these pairs. That is, if p₁ and p₂ are within ε then p₂ and p₁ are also within ε, and both must be counted towards the total number of points within ε of each other. One must also add to the total count the distance between a point and itself. E.g., distance(p₁, p₁) = 0 will always be within ε. (these requirements make the total count easier to compute, as these are considered corner cases, when going by the normal O(N²) approach)

Also note that the value of the seed for the random number generator is to be kept constant as we need the same results to compare and verify. For instance, with the seed set as 72, these are two different total count values for an N of 10³ (for testing purposes) and 10⁵, with slight variations in the numbers depending on the OS: (the math library’s rand implementations differ a bit for Linux and OS X)

N	ε	Linux Count value	OS X Count value
103	5	1102	1092
103	10	1356	1310
105	5	879688	881058
105	10	3211140	3213704

There are two separate program versions that I worked on - namely the unoptimized brute force approach (for comparison) that runs in O(N²) time complexity, and an optimized approach (whatever one would want to throw at it to get the best performance out of it) that betters it. For both, the program takes as input on the command line a value for ε (declared as a double-precision float) and it outputs the total number of point comparisons that are within ε.

Brute Force Approach

The straightforward, unoptimized approach would be to simply use two nested loops running for N iterations each, where N is the number of points. Each point searches for every other point, computing the distance between them, which results in a large computation time, especially for the sequential version without optimization (and especially for larger values of N, of course).

For the parallelized version, the omp directives parallel and for are used, with the loop variables and the Euclidean-distance-value holding variable being made private and specific to each thread to avoid race conditions. I used a reduction on the counting variable (which would be private as well) since that would be the best option here.

Observations (click to extend)

I made a table accounting for the different possibilities and I observed that my parallel efficiency when running with 6 cores is pretty good when going without (explicit) compiler optimization (-O3), and is decent with compiler optimization applied, but definitely less in comparison to the former, as expected. This is due to the fact that a highly-optimized program affords less opportunity for parallelism to be effective. It may be that the balance of the serial vs. parallelizable parts is changed, like the scalability can be limited by the OpenMP overhead and the fact that only a portion of code is parallelizable (Amdahl's law applies here), in which case compiling without optimization would increase the parallel time, thus reducing the percentage of the overhead plus serial part. On the other hand, the parallelizable part of the code represents, after optimizing, a smaller fraction of execution time. Thus, by Amdahl's law, it makes sense that improving the execution time of that part of the code by parallelization should have a smaller effect on the total execution time, and thus the speedup or parallel efficiency metric won’t scale along well with the (compiler) optimization.

Another reason I can think of to explain this is the effect of a system bottleneck such as the memory bus (on typical consumer hardware like mine, all of the cores share one memory bus, so using more threads does not give me more bandwidth here, and this is the bottleneck, which affects speedup) that creates the same scenario.

To elaborate, there's a certain amount of memory bandwidth that the execution of the algorithm is going to require. The less optimized the code, the more internal CPU machinations dominate the run time. The more optimized the code, the more memory speed dominates the run time. Since unoptimized code is less efficient, more cores can run it before the system memory bandwidth gets saturated. Since the optimized code is more efficient, it gets its memory accesses done faster and thus puts a heavier load on the system memory bandwidth. This makes it less parallelizable.

In conclusion, the slowest configuration (implicatory of going without optimization) would usually give the best parallel scaling. (speedup, efficiency)

Also note that for the case without compiler optimization, I got a parallel efficiency greater than 1, which doesn’t look theoretically possible (although it’s just slightly above the ideal number), but is completely possible due to superlinear speedup, which is usually caused by improving the cache usage, i.e. the total amount of work my processors do is strictly less than the total work performed by a single processor. This is happening here because the original sequential algorithm performs real bad, and using the parallel version of the algorithm on one processor will usually do away with it.

To elaborate, this is due to the fact that modern processors have their set of fast memory and relatively slower but shared memories. Each processor has its own L1 cache, which is the fastest, and then they will have their L2 and L3 caches as well, which will be slower, but then they are shared. Typically what is happening here on a single core run is that my processor might have tried to keep the data I was using in the fast memory or cache, and I can safely say that the amount of data is larger than the amount of fast memory I have, so it takes a long amount of time (also no data is shared, it’s just one processor doing everything!). But if I use say N processors, then I’ll have N times the amount of fast memory (consider the L1 cache), and in this case, more data will fit in the fast memory which makes it possible to take less time (thus amount of work) on the same task (with data sharing possible for the relatively slower L2/L3 cache), and achieve a higher parallel efficiency in total.

This number could probably change if I reduce my problem size (going for a smaller value, instead of taking N = 1e+5) such that it fits into my cache for one core, or if I increase the number of calculations on the point data.

Also, I think that OpenMP internally might use a parallel algorithm that uses some search like a random walk as well, and the more processors that are walking, the less distance has to be walked in total before we reach what we are looking for, which is another possibility that could potentially explain this behaviour, although I would like to think that my first reason is the actual one.

Optimized Approach(es)

There are several things that I thought of and tried out, and some of them were optimizations, while some were not, and some would be, but I am not sure how to implement them. I’ll be going through them one by one.

The very first optimization I performed was to avoid the computation for the double-counting for a pair of points i.e. to avoid counting the distance between (x₂, y₂) and (x₁, y₁) if the distance between (x₁, y₁) and (x₂, y₂) is known or being computed. I paired this optimization with the one where I avoided self-counting of points. I achieved this by running my inner loop based on the outer loop’s index (i.e. j is based on i, considering that i is for the outer loop, which only needs to run until the second last element or N - 1 too), and by adding a one to that to skip the initial iteration that would evaluate to be the point (i, i). In this way, if the inner loop is limited to perform only from the next iteration (j = i + 1), I will always have a start that is smaller, and by default eliminate the self-count. And again, this tends to be an optimization since counting the distance to itself is a wasted operation, and I will have N points being skipped this way, which I can just simply add to my count at the end.

The search would be reduced quite a bit in this way, and the only change I had to make for the counting to be accurate was to double my count at the very end while printing, and to add N to that (to account for the self-counts), i.e. to print 2*(count)+N. Could have gone for count +=2 instead of count++ to avoid the single multiplication operation on count while printing, but that wouldn’t really make any difference.

I took things step by step and thought about optimizing every statement possible. I know that using for-loops could add an extra jmp/cmp-test in some cases, but that might not be reproducible everywhere, and since OpenMP doesn’t have a variant for while loops, this was out of the question.

What I was sure of that would have been an optimization is if I could sort the points by some criteria, since due to successful branch prediction then, the processor doing the branching on the if-conditional comparison would take barely any time with the sorted sequence of points, whereas, for a random sequence, the branch chosen varies randomly, and could be a few orders of magnitude slower.

The problem though, lies in the fact that I am dealing with two dimensions collectively, or rather x and y values both, and not just one. I can sort the x points or the y points (tried that using qsort from the standard library, and only one would work at a time, as one can only sort a one-dimensional array with a single metric), but I was stuck wondering how to sort both collectively in a way, given the absence of a single-variable link in between those two. Eventually, I gave up on optimizing this.

I also spent some time trying to optimize the math functions (pow and sqrt) being used for the computational part, given that I am attempting to optimize an algorithm which is effectively based-off the pythagorean theorem that introduces these rather compute-intensive functions when used repeatedly for a large array of points.

I tried using simple multiplication (i.e. of the form x*x) for obtaining the squares instead of using the pow function from the math library, but that turned out to be slower. Separate implementation of the squaring as a function while using just bitwise operations (mostly bit shifts, and a logical and) didn’t help as well.

Next, I tried to optimize the sqrt function, including implementations involving a binary search and bitwise operations, but as it turns out, that didn’t quite work well in terms of efficiency (as compared to the standard math library’s implementation) and precision, even though I managed to get pretty close to the correct answer after some trials. (for instance, I used multiple rounds of Newton-Raphson’s method to get more precision, inspired by Quake 3’s inverse-sqrt algorithm)

I was curious to see if the sqrt on an optimize (while using compiler optimization at the O3 level) is processed to an fsqrt opcode, but going through the pile of assembly (performed the comparative analysis via Godbolt) was nothing less of a nightmare, in addition to that being bemusing. (also realized that reading through optimized assembly and then reverse-engineering it to gather optimizations that could potentially be programmed into the actual code instead of the compiled binary was kinda pointless to do here). The standard library’s implementations were better for almost all cases, and even if I could get some optimization, I believe it would be just slightly better or kind of micro-optimized.

Soon after, I realized, why do I even need the square root operation? I could have simply squared both sides of the equation i.e. going with ε² > (y₂ - y₁)² + (x₂ - x₁)² instead of the square rooting on the right hand side of the inequality for ε on the left hand side. Eliminating the square rooting operation(s) indeed felt like a neat trivial hack, as squaring is cheap, but square rooting is expensive. A simple optimization to think of that was, but in practice that really helped reduced speeds by quite a bit as well (combined with the loop optimization from above, I was able to reach a speed of 0.6 seconds while using compiler optimization and around 30-ish seconds without)

Just to reiterate up till here - there is a reduction in the number of points compared since I avoided double-counting for a pair of points and self-counting points, which reduces the search from O(N²) to somewhere in between that and O(NlogN). There is also quite a bit of reduction in floating-point operations, primarily because I am not using the sqrt function, which takes one floating-point operation (and that would be 100,000 operations off the computation for 100k points), and supposedly less than four clock cycles (no more than four on modern CPUs) each time it is used.

After this point, while I felt I could optimize further (as greedy as one could get) on the current code, I realized it wouldn’t make much of a difference and I have to think of other ways of visualizing and tackling the problem to get a substantially big difference. So I tried to think of different ways to approach the distance counting and representation in 2D, and jotted them down on paper.

The very first thing that came to my mind was to just search for points at ε distance from a point when considering each point in a loop, i.e. I was wondering if a point inside a circle (at ε distance from the point, which acts as the center) algorithm could be run against each point, to limit the possible area of the grid to search. In order to establish the region inside the circle, I thought of a square grid that encloses the circle, with some extra regions left out as outliers. I kinda got this circle inside the box idea while thinking about Monte Carlo estimation of Pi, but again, this doesn’t completely fit the box, unless I make a partition and get some outliers (kinda like the dbscan algorithm).

While at first I was wondering if I should even use a data structure or something that holds/records a value for memoization, (like I thought I didn’t need it because I’m just counting the value, not using it later) it seemed like I had to go with spatial partitioning with a grid-like structure in play to achieve this. I felt this was pretty close to a minimal search, like every point just searches up the grids which lie within and around its radius, and not the entire grid. It’s like thinking of everything to lie in a grid, instead of just each point looking out for each point like in the regular approach (not only the brute force unoptimized approach with two loops until N making it O(N²), but also with the slight optimization of avoiding double counting and the points itself, like that still is a approach relying on each point looking out for each point!)

I went about creating a 2D grid-like structure wherein all the points lie within that, with ‘buckets’ (basically a box/cell with intent to store something, in this case it would be points) created after some memory allocation (I realized that memory management would be crucial here!). When I would iterate through each point, I would just check for the grids that encloses the entire circle governed by the search radius ε. As to checking through the grid, we need to know the dimensions, in terms of our circle’s radius ε. I was able to figure that by drawing on paper, and now on paint to show this to you in a presentable format:

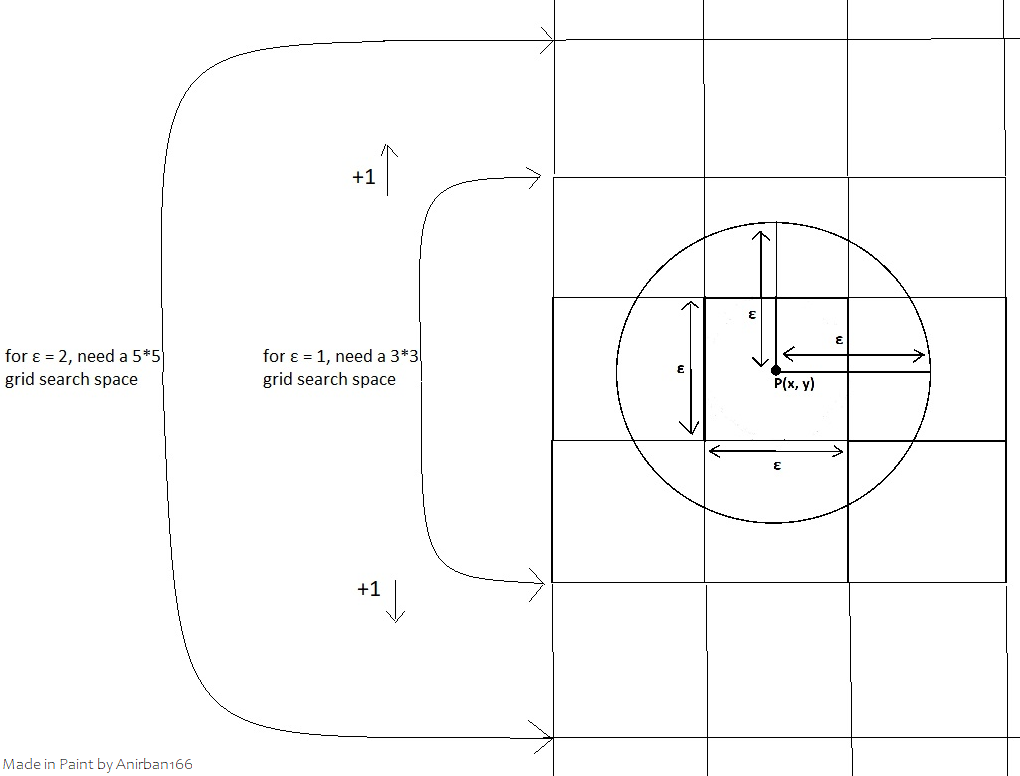
In my drawing above, you can observe that I’m considering a point to be at the middle of the box (which is actually the worst case. why? - coming to that after this paragraph*), and then if we consider ε to be the edge of the square governing it, then you’ll notice that you need a square grid of 3*3 to completely contain that circle. If we double ε, i.e. we consider it to be twice the edge/side length of a grid square (again, ε means the circle’s radius, or the search radius for a point, with the point being the center of the circle here), then you’ll notice that we need to increase our boxes by one each on all sides, (+1 in all four directions, or +2 vertically/horizontally) which gives us a (3+2)*(3+2) = 5*5 dimension grid search space. This is, but while thinking geometrically on pen and paper. I need to have a value to plug in my program concerning my input ε, and I got that by figuring the (simple) pattern - It’s a (2ε+1)*(2ε+1) grid search space for each point for an ε value. Thus, the coordinates forming my square grid would be (0,0), (0, 2ε+1), (2ε+1, 0) and (2ε+1, 2ε+1).

*I mentioned that the middle point case (circle lies at the middle of a box) is the worst-case scenario, since that’s when we will have to do the maximum search (for the most number of boxes or cells) - but for a slighter better case, say the point lies exactly on the intersection of two edges or sides of a box that we are searching (and notice that we were searching every other box adjacent by side/diagonal, or in other words a grid that completely encloses the circle of radius ε, which makes it a or 3*3 grid for the previous case), then we’ll only have to search 6 boxes. Could have that as an optimization for later (like if points actually lie on the grid, minimize the search space), but first I’ll need to take care of the regular approach for this (i.e. taking the worst-case scenario in mind, and using that for all cases)

This was one way to think of the problem on paper, but there was another way to think of this that kicked in my mind, which was just the reverse of this ‘circle inside a square grid’ kinda approach, i.e. the ‘square inside the circle’ approach:

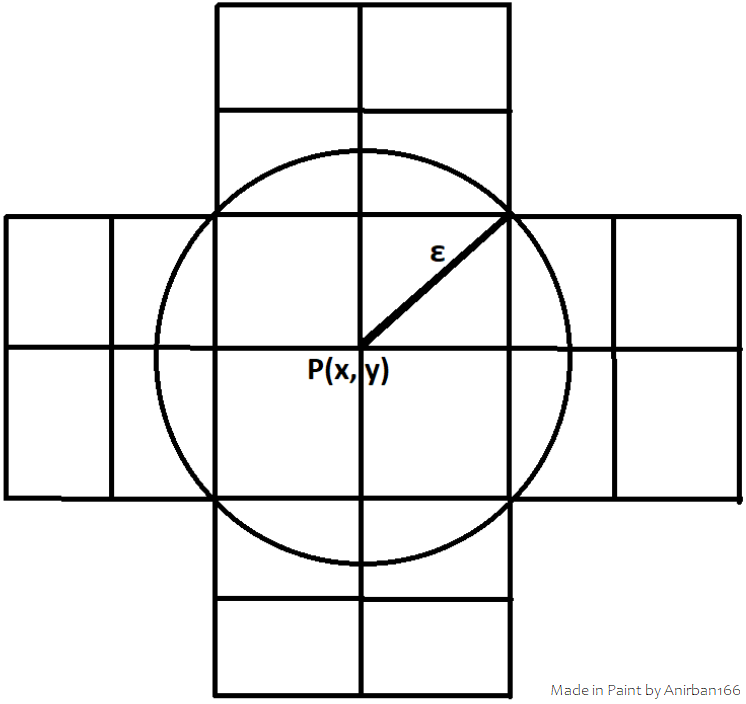
As you can observe from my figure above, I partitioned the square inside the circle into four equal (roughly, as per my drawing in paint) squares, because that would be the ideal bucket size as I figured. If I consider the big square as one bucket, then I would waste searching for half of the bucket size (or big square size) for the adjacent buckets that I have to search for completely enclosing the circle. If I go with this quadrant of a bucket size, I don’t have to search for those two extra quadrants (for e.g. in my figure above, it would be the pair of squares to the extremities in each direction). This way, the circle contains four complete buckets (for the best-case corner point) and eight partial buckets (two in each direction, like the top, bottom, left, and right to enclose the region inside the circle). Here a corner point gets all the points in the four surrounding buckets for free, but I still have to check the points in the eight bordering buckets. Any point within a given square bucket is trivially within ε of every other point within the bucket, including those on the edges and the four corner points. (and then I just have to compare the points in adjacent buckets)

At this point, it even seemed like creating a sparse array with arbitrary lookup would be fine, instead of making a grid that contains every possible bucket. I created a hash table (for this sparse array) where the inputs were the coordinates of the bucket, and the output was an index to a hashmap (basically a lookup table array), and within there I stored the points array. I made a hash function that takes the x and y coordinates of the bucket - and generates some value. I then plug this into my hashmap and get out a pointer when there isn’t a bucket at the hash yet. I keep on dynamically resizing my bucket (or array of point structs) as more points get added. After checking a particular bucket, I removed the current bucket in its entirety since its existence would no longer be necessary.

One initial issue that popped into my mind here was that I initially couldn’t apply the optimization of using epsilon-squared directly here (from my previously optimized approach). So I re-thought this in terms of ε², and I figured that if I divide the grid into squares of side length $\sqrt{\epsilon }$, then every pair of points within a bucket will be within one epsilon distance of each other guaranteed, and a point on an edge or a corner within range of every point for the buckets it touches. For the worst-case scenario of two points on opposite sides of a bucket, it would be $\sqrt{2}$*(side length), or in other words, the side length would be ε*(2)^-1/2.

While that was fixed, one thing I couldn’t fix was the wrong count value that I was getting. Clearly, there were multiple overlaps, and I reasoned there were many ways it could happen. For a simple example, a point lying within the intersection of two bucket edges would be triple counted.

At this point, I thought to make my buckets more granular (using RAM than stack) and I tried to figure out what size the buckets need to be for N = 100k points by observing the extremes on what the maximum value is for the largest bucket, based on a seed of 72. If I can preallocate to that size then I could reduce the extra space.

I also thought of going with a circle drawing algorithm since I like to think that way, and also when parallelizing, I could then make the threads draw divisions of the circle (like for 8 threads they could each draw one octant) to make the speedup better. I thought of doing a bounds within a circle of radius epsilon but I eventually ended up doing what I was inclined towards, i.e. splitting the circle into quadrants, so when searching for the four corners, I could collect the points and estimate which ones are out of bounds. Basically what I was trying to think of here is like a hack to know where the points already are (since the seed is fixed, I can expect the same distribution every time) and then figure out the areas where they do not need to be searched, to minimize time searching for those areas, and to minimize space by not creating buckets for those. Then my program can calculate this maybe on the first pass and then cache it for subsequent passes. I managed to create such a circular ring formation of points for a search radius, and here’s what an example of such a pattern looks like:

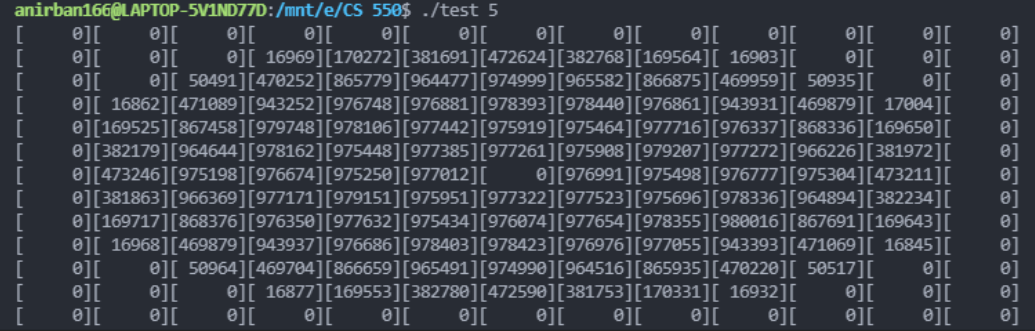
With the bucket structure into play and with the search for adjacent buckets, I’m able to reach a very fast runtime (expected, sort of) of under a second with ε = 5 and under two with ε = 10, without compiler optimization. Note that one would have to precompute the offsets to account for miscounts.

Anirban

11/14/2021